AcWing 788. 逆序对的数量 *

[toc]

感谢微信群群友的解答：黑桃皇后、五个结晶水、但为君故

现在我也是似懂非懂的，看一天了······太菜了，hhh。

AcWing 788. 逆序对的数量【简单】*

一、题目描述

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。
逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式
第一行包含整数 n，表示数列的长度。
第二行包含 n 个整数，表示整个数列。

输出格式
输出一个整数，表示逆序对的个数。

数据范围
1≤n≤100000，
数列中的元素的取值范围 [1,109]。

输入样例：

6
2 3 4 5 6 1

输出样例：

5

二、解题方法

3

1、暴力

/**
 * @version:
 * @author: @Akari
 * @date: 2024-01-24 15:44:13
 **/
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define endl '\n'
using namespace std;
typedef long long LL;

const int N = 1e5 + 10;
int n, q[N];

int main(void)
{
    LL res = 0;
    scanf("%lld", &n);
    for (int i = 0; i < n; i ++ ) scanf("%lld", &q[i]);
    
    for (int i = 0; i < n; i ++ ){
        for (int j = i + 1; j < n; j ++ ){
            if (q[i] > q[j])
                res ++;
        }
    }
    printf("%lld\n", res);
    
    return 0;
}

毫无悬念：Time Limit Exceeded。

2、归并

大概理解，主要是理解 res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r)，就是先求出第一次平分左右两边的逆序数，再分别对左右两边进行平分求逆序数，一直递归下去。

也可以用 void 作为返回类型，全局定义一个 LL res = 0;。

/**
 * @version:
 * @author: @Akari
 * @date: 2024-01-24 15:25:09
 **/
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define endl '\n'
using namespace std;
typedef long long LL;   // 必须用 long long，防止爆 int

const int N = 1e5 + 10;
int n, q[N], tmp[N];
LL merge_sort(int q[], int l, int r);   // 也要改为 long long

int main(void)
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> q[i];
    cout << merge_sort(q, 0, n - 1) << endl;
    
    return 0;
}

LL merge_sort(int q[], int l, int r){
    if (l >= r) return 0;
    
    // 递归处理左右两部分
    int mid = l + (r - l) / 2;
    // 递归排序！（将序列一直分，拆封成单个，即为有序）
    LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);
    // 当前层的结果是回溯的上一层两边相加的结果

    // 归并的过程
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else {
            tmp[k ++ ] = q[j ++ ];
            res += mid - i + 1;     //满足逆序对条件
        }
        
    // 扫尾
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];
    
    // 物归原主
    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
    
    return res;
}

3、树状数组解法 *

AcWing 788 逆序对的数量 之 树状数组 解法 - 糖豆爸爸 - 博客园

看大佬blog，还可以这样写，不过我还没学到，先开个坑······

4、线段树+静态数组 *

AcWing 788 逆序对的数量 之 树状数组 解法 - 糖豆爸爸 - 博客园

同上。

三、具体分析

1、答案的数据类型

Q： 逆序对最多有多少？
A： 当数列逆序时，逆序对最多，比如：[5, 4, 3, 2, 1]，所以最多有 res = n-1 + n-2 + ··· + 2 + 1 == (n*(n-1))/2
本题 1<=n<=10000，所以 res = 100000 * (100000 - 1) / 2 ≈ 1e10 ÷ 2 = 5 * 10^9
而 int 极限为 2147483647，约为 2 * 10^9，所以会爆 int，需要用long long

$fileName

2、利用归并求逆序对

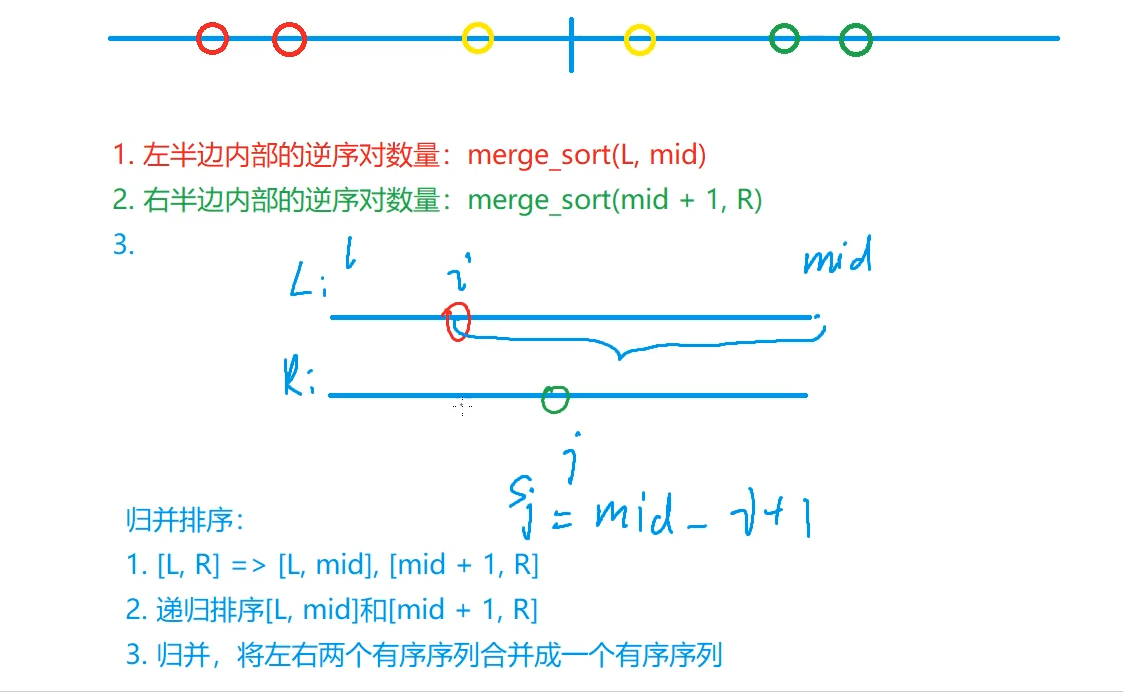
$fileName

在归并两个子数组时，有三种情况:

（1）、逆序对在左边（红色）
这在调用左侧子数组进行递归时，已经完成了统计，自己不管。（内部问题内部解决）
（2）、逆序对在右边（绿色）
这在调用右侧子数组进行递归时，已经完成了统计，自己不管。(内部问题内部解决)
（3）、逆序对在左侧和右侧（黄色）
这个需要自己来处理，对于右侧的黄色圆，那么在左侧的黄色圆及左侧黄色圆后面，一直到中线的所有数，都是比右侧黄色圆大的，就是有 mid - i + 1 个逆序对。

可以结合代码来理解原理，其实就是在归并时，只处理合并数组中大小反着的两个数字，一旦发现前面的数字比后面的数字大，就是发现了一个逆序对。同时，由于归并排序的特点，两个要归并的数组是内部有序的，所以，意味着左侧当前数字及其之后的一直到左侧集合结束的所有数字，都比右侧当前数字大！那么个数就是 mid - i + 1 个，其中 l <= i <= mid 。

3、内部问题内部解决什么意思？

@Arsene7777：

其实本质还是递归跟分治。
假设给你两个有序列的数组 A, B，那么显然，A 和 B 的逆序数就都是 0 对不对。所以将 A, B 按照顺序接成一个新的数组的逆序数，是不是就等于求y总视频中所讲的黄色逆序数的个数？
本质就是 C 由 A, B 构成，那么对 C 求某些特定的性质，可以等价于 对 A 求（红色）加上对 B 求（绿色），再加上将 A，B 整合之后产生的性质（黄色），然后又可以将 A 看作由更小的 E，F。而当数组不可以再划分的时候，即只要一个元素的时候，就是我们递归的尽头了。
所以我觉得归并的本质还是求黄色的逆序数，因为 A 红色的逆序数可以等于 A 的红色+黄色+绿色，而最底层的红色和绿色都为 0，所以本质是求黄色。

@劲能神佑：

在这里要理解逆序数的本质，逆序数是用来描述这个数列相对于排序后的混乱程度的（逆序数就是每次交换一变成排序后数列的次数（和冒泡的次数一致））。那么只要是排序方法，理论上都可以做（比如快排把那个x参照点设为最左端就可以做，复杂度（o^2））

4、用归并排序的原因（难）

归并排序天然适合解决逆序对的计算问题，因为归并排序的关键步骤是将两个有序的子数组合并成一个有序的数组。在这个过程中，如果左边数组中的某个元素大于右边数组中的某个元素，那么左边数组中该元素后面的所有元素都会与右边数组中的这个元素构成逆序对。
通过在归并排序的过程中统计逆序对的数量，可以高效地解决逆序对计算问题。因为归并排序的分治策略使得每个子问题都能得到解决，而逆序对的数量可以在合并的过程中被有效地计算出来。

四、总结

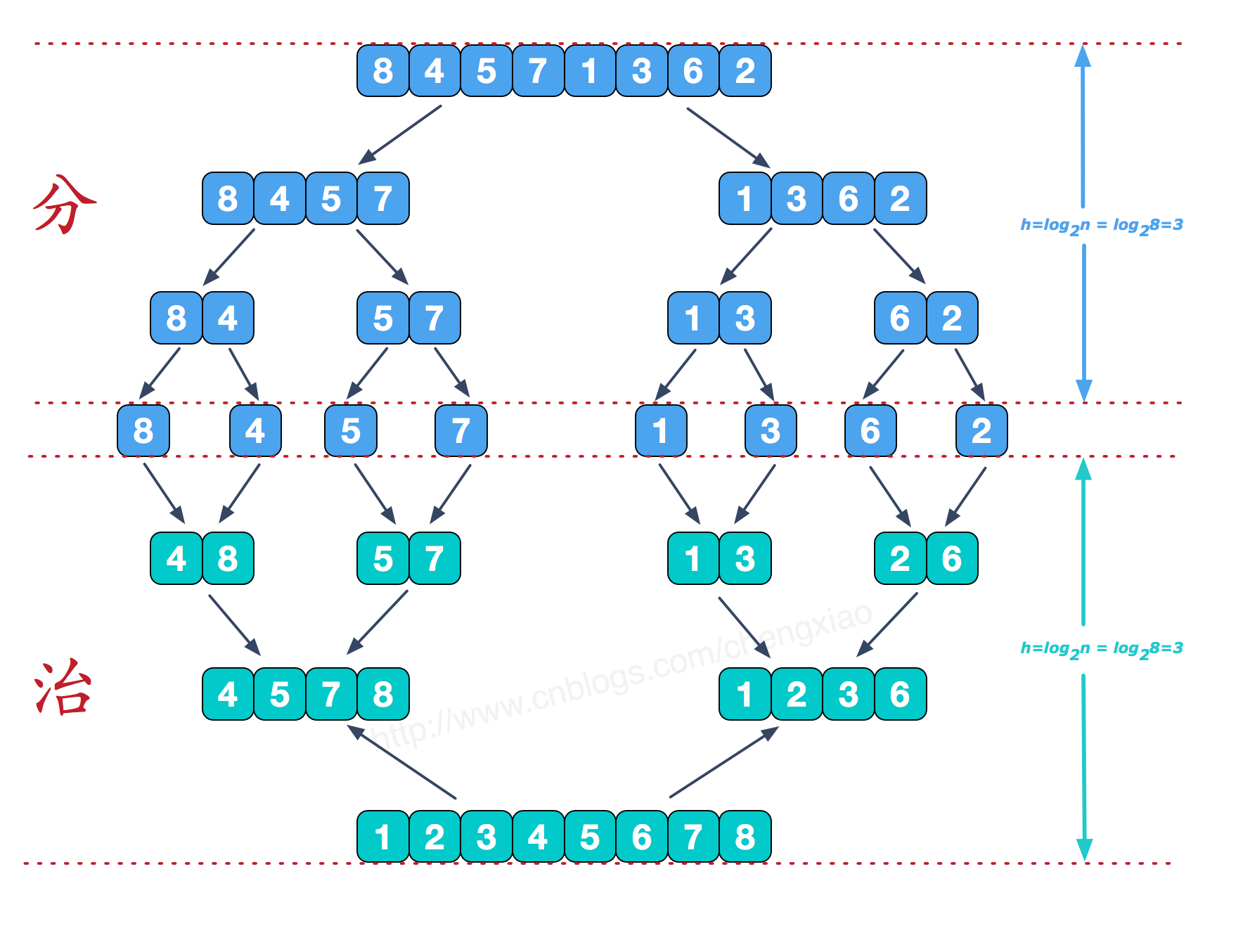
可以借助这张图理解：

$fileName

1、第三种情况利用了归并的特性

Q： 是不是左半部分和右半部分分别当成一个新的数列进行归并处理，而第三种左右两边都有的情况恰好利用了归并合并的特性？
A： 是的。

在归并排序中，递归地将原始数组分割成更小的子数组，然后对这些子数组进行排序。在合并的过程中，利用归并的特性确保有序的子数组正确地合并成整体有序的数组。
对于逆序对的问题，正是因为归并排序的特性，可以有效地在合并的过程中统计逆序对的数量。具体来说：

  1. 当递归处理左侧子数组时，逆序对的统计已经在更深层次的递归中完成了。左侧子数组在当前层次是有序的。
  2. 当递归处理右侧子数组时，逆序对的统计同样在更深层次的递归中完成了。右侧子数组在当前层次是有序的。
  3. 当左右两侧都有序时，合并的过程中，我们可以通过比较左右两侧的元素大小来统计逆序对的数量。这是因为在左侧有序的情况下，右侧的某个元素比左侧当前元素小，就形成了逆序对，数量为左侧剩余元素的个数。

这种分治和归并的结合，确保了逆序对问题可以在归并的过程中高效地解决。左右两侧各自有序的特性为这一算法提供了便利，而第三种情况则充分利用了归并排序的特性来统计逆序对数量。

2、左右两半进行处理时其实最后也是第三种情况

换句话说：第三种情况就是处理前面 2 种情况的已经排好序的数组，并在合并的过程中统计逆序对的数量。

当左侧子数组和右侧子数组都是有序的时候，在合并过程中，可以利用归并排序的特性，比较左右两侧的元素大小，以统计逆序对的数量（也就是模板里的归并过程）。此时，左侧子数组和右侧子数组各自都是已经排好序的，因此可以在合并的过程中通过比较元素大小，统计逆序对的数量。统计在合并的过程中进行，而不是在递归的过程中。

3、递归函数的作用

你可以自己写个例子看一下，就像是后序遍历一样。

递归函数在归并排序中的作用是对子数组进行排序：

  1. 递归地将数组分解为更小的子数组： 先检查数组的长度，如果长度超过 1，就将数组分成两半。然后，递归地对这两个子数组调用自身，将它们分解为更小的子数组，直到每个子数组的长度都为 1。
  2. 对子数组进行合并排序： 一旦数组被分解为长度为 1 的子数组，递归函数开始合并这些子数组，同时进行排序。通过调用归并函数来完成，归并函数的任务是将两个有序的子数组合并成一个有序的数组。

在这个过程中，递归函数不仅会进行拆分，还会在合并的时候进行逆序对的统计。通过递归的方式，整个数组最终会被分解为越来越小的子数组，然后逆序对的数量也会被统计和合并，直到最终得到完整有序的数组。
因此，递归函数在归并排序中的主要作用是将大问题分解为更小的子问题，并在递归的过程中解决这些子问题。递归的停止条件是子数组长度为 1，此时递归回溯，对子数组进行合并排序。

4、本质

从根本上来说只是在归并排序的合并过程中求出两个子数组的逆序对数，而每个子数组也都是左右递归形成的，这样只要通过递归到最深层的时候回溯的过程就可以对合并过程得到的每一个子结果进行累加就是答案了

Q： 是不是左半部分和右半部分分别当成一个新的数列进行归并处理，而第三种左右两边都有的情况恰好利用了归并合并的特性
因为合并的时候就是左右两半进行比较嘛，而左右两半进行处理时其实最后也是第三种情况
A： 是的。
当前层的结果是回溯的上一层两边相加的结果

通过分治和递归，最深层的单个元素 return 往回，就是两个元素，这两个元素是来自两个数列的，也就是黄色圈的情况。本质上，红色圈和蓝色圈，各自的情况是不存在的，这是借助计算机代码的特性所造成的

Q： 既然本质是黄色圈之间比较，为什么还要有红色圈和蓝色圈呢？或者说，我不明白为什么是res是两种情况相加。
A： 这里是后序遍历，所以递归到最后一层（也就是一个数的时候）才开始merge，红色圈和蓝色圈就是依靠黄色情况下算出来的，所以最终结果就是res += 左半边 + 右半边。
Q： 我觉得是不是：递归到最深处，只有第三种情况，前两个就是描述这个递归的过程，只是用来帮助理解，事实上不存在。归并排序的递归过程的边界就是区间只有1个数，所以就是第三种 两边相加的情况。
A： 以左边的举例，左边的递归到最深处只有黄色的情况 ，这个结果返回到上一层之后，它的值就是红色。
A： 说的是没问题的，其实意思就是不断递归找黄色部分进行加和的，红色和蓝色部分只是大体上的概念。
A： 这样理解 那些红色和蓝色的情况在最后递归之后 还是会变成 后面那些 较小的数组的黄色情况