第一讲 基础算法 - 03 二分

二分

一、简介

二分搜索是一种在有序数组中查找某一特定元素的搜索算法。

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

二分查找算法在最坏情况下是对数时间复杂度的，需要进行 O(log n) 次比较操作。二分查找算法使用常数空间，对于任何大小的输入数据，算法使用的空间都是一样的。除非输入数据数量很少，否则二分查找算法比线性搜索更快，但数组必须事先被排序。尽管一些特定的、为了快速搜索而设计的数据结构更有效（比如哈希表），二分查找算法应用面更广。

二分查找算法有许多种变种。比如分散层叠可以提升在多个数组中对同一个数值的搜索的速度。分散层叠有效的解决了计算几何学和其他领域的许多搜索问题。指数搜索将二分查找算法拓宽到无边界的列表。二叉搜索树和B树数据结构就是基于二分查找算法的。

二、分类

2.1 完全匹配（简单）

形如：-1 0 3 5 9 12

使用条件：

  • 线性表中的记录必须按关键码有序
  • 必须采用顺序存储
  • 数组中不能有重复元素，必须保证返回值唯一

这种就是最简单的二分，单调无重复数组中找目标值。
完全匹配的二分搜索只对有序数组有效。二分搜索先比较数组中位元素和目标值。如果目标值与中位元素相等，则返回其在数组中的位置；如果目标值小于中位元素，则搜索继续在前半部分的数组中进行。如果目标值大于中位元素，则搜索继续在数组后半部分进行。由此，算法每次排除掉至少一半的待查数组。

2.2 大致匹配（难）

比如：1 2 2 3 3 4 12

使用条件：

  • 线性表中的记录必须按关键码有序
  • 可以有重复元素

以上程序只适用于完全匹配，也就是查找一个目标值的位置。
而大致匹配的二分更适用于需要找到大致匹配（即接近目标值）的情况，例如查找范围内的上限和下限，但是实际使用中还会有其它情况。

三、复杂度分析

平均时间复杂度 O(log n)
最坏时间复杂度 O(log n)
最优时间复杂度 O(1)

四、整数二分

完全匹配的二分已经详细写过 blog，不再叙述，本篇重点叙述大致匹配的二分。

4.1 yxc

4.1.1 基本思想：

有单调性一定可以二分，但是可以二分的题目不一定非要有单调性。找到一个边界将区间划分为两部分，使得一部分满足，另一部分不满足。
1
这里的两个边界点就对应两个模板写法。

第一种情况：红色边界点
check (mid) 判断 mid 是否满足红颜色的性质。注意 mid = ( l + r + 1) / 2 以及更新区间时的 mid 和 mid-1。
第二种情况：绿色边界点
check (mid) 判断 mid 是否满足绿颜色的性质。注意更新区间时的 mid 和 mid+1。

$fileName

4.1.2 注意点：

如果是 l = mid ，就要在 mid 中补上 +1。
如果是 r = mid ，就不用补 +1。

补上 + 1 的原因在于：
如果不补上的话，当 l = r - 1，由于 C++ 是下取整的，所以 mid = l，更新后区间没变，会导致死循环。
也就是说：

  1. 当 l 和 r 只相差 1，即 l == r - 1 时。mid = (l + r) / 2 = l。若此时 a[mid] 满足左边边性质，则有 **(l, r) → (mid, r) = (l, r)**，搜索区间不变，则陷入死循环。
  2. 若 + 1，则下取整变成上取整，此时 mid = (l + r + 1) / 2 = r。若此时 a[mid] 满足左半边性质，**则有 (l, r) → (mid, r) = (r, r)**，则结果为 r，不会陷入死循环。

4.1.3 总结：

$fileName

二分的本质是寻找边界：如果一组数能根据某个性质一分为二，则可快速通过二分找到边界。它有两种模板：寻找左半边的边界和右半边的边界。
实际运用时，先不考虑用哪个模板，而是先写 check() 函数，然后写模板（不考虑 mid 是否 + 1），写到 if(check(mid)) 时，再考虑满足 check(mid) 的段是在哪一边：如果在左边，则填 l = mid；如果在右边，则填 r = mid。然后填出 else 的部分，如果存在 l = mid，则要在 mid 声明处 + 1；反之不补。

4.1.4 代码模板：

这两个函数的 check() 函数不一定相同，根据题目设计。

  1. 左闭右闭 [0, n - 1]
  2. 默认升序排列
    如果是降序，把符号 对称 改过来即可。比如 >= 改为 <=**，**<=** 改为 **>=
  3. bsearch_upper() 中，mid = l + (r - l) / 2 + 1：
    一个mid = (l + r) >> 1
    一个mid = (l + r + 1) >> 1
    加不加 1，完全取决于 l = mid 还是 r = mid
    l 等于 mid 时必须 +1 向上取整，不然会陷入 l = l 的死循环
    r = mid 时候不用加 1，因为下一步 l = r 直接会退出循环
bool check(int mid, int x) {/* ... */}   // 检查 x 是否满足某种性质

// 寻找右半边边界(下限), 区间 [l, r] 被划分成 [l, mid] 和 [mid + 1, r] 时使用
int bsearch_lower(int l, int r, int x){
    while (l < r){
        int mid = l + (r - l) / 2;
        if (check(mid, x)) r = mid;    // a[mid] 满足右半边性质, 应在 [l, mid] 继续寻找
        else l = mid + 1;   // a[mid]不满足右半边性质, 应在[mid + 1, r]继续寻找
    }
    return l;   // 二分结束后 l == r. 如果一定存在右半边的边界, l和r 都是结果. 如果不一定存在右半边的边界, 需要做 if 判断
}

// 寻找左半边边界(上限), 区间 [l, r] 被划分成 [l, mid - 1] 和 [mid, r] 时使用
int bsearch_upper(int l, int r, int x){
    while (l < r){
        int mid = l + (r - l) / 2 + 1;  // 让下取整变成上取整, 避免 l = mid 出现死循环
        if (check(mid, x)) l = mid;     // a[mid] 满足左半边性质, 应在 [mid, r] 继续寻找
        else r = mid - 1;   // a[mid] 不满足左半边性质, 应在 [l, mid - 1] 续寻找
    }
    return l;   // 二分结束后 l == r. 如果一定存在左半边的边界, l 和 r 都是结果. 如果不一定存在左半边的边界, 需要做 if 判断
}

4.2 董晓算法

图中下标是从 1 开始的！而一般都是从 0 开始的！重要的事情说三遍！
图中下标是从 1 开始的！而一般都是从 0 开始的！重要的事情说三遍！
图中下标是从 1 开始的！而一般都是从 0 开始的！重要的事情说三遍！

老实说，我喜欢这种，很容易理解。
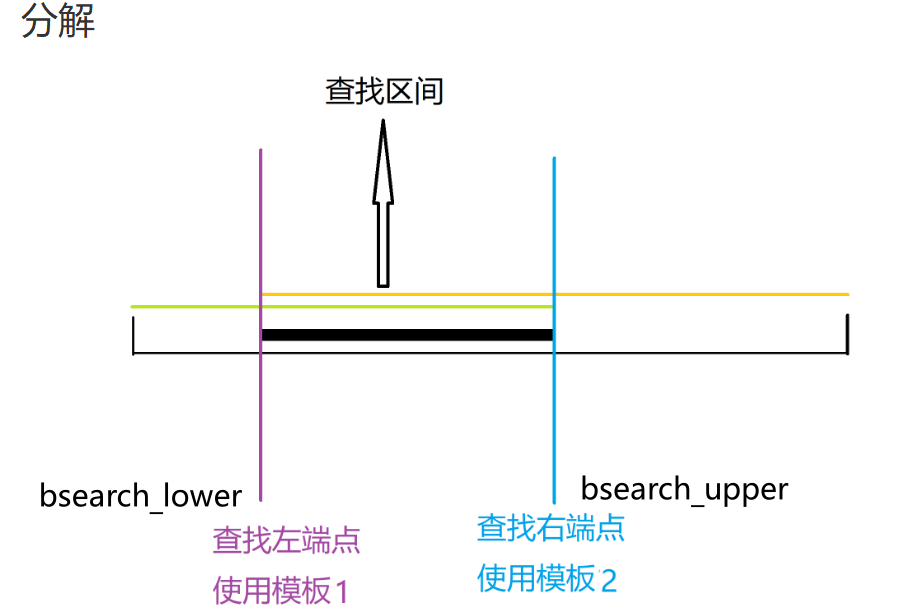
如图所示，以查询上限和下限为例：（别的情况类似，只是判断条件变了而已）：

1. 基本思想：

本质上，这种二分查找的思想是基于有序数组的特性，通过每一步将搜索范围缩小一半的方式，快速定位目标值或满足某个条件的元素。
基本思想的关键在于通过比较目标值与中间元素的大小关系，不断调整搜索范围。在每一步，通过 check() 函数来判断中间值是否满足条件，根据判断结果，动态地调整搜索范围的左右边界。
总体而言，本质上这种二分查找是一种分治策略，通过将搜索范围一分为二，然后根据目标值与中间值的关系，决定舍弃一半的数据，从而在较短的时间内快速找到目标值或满足条件的元素。

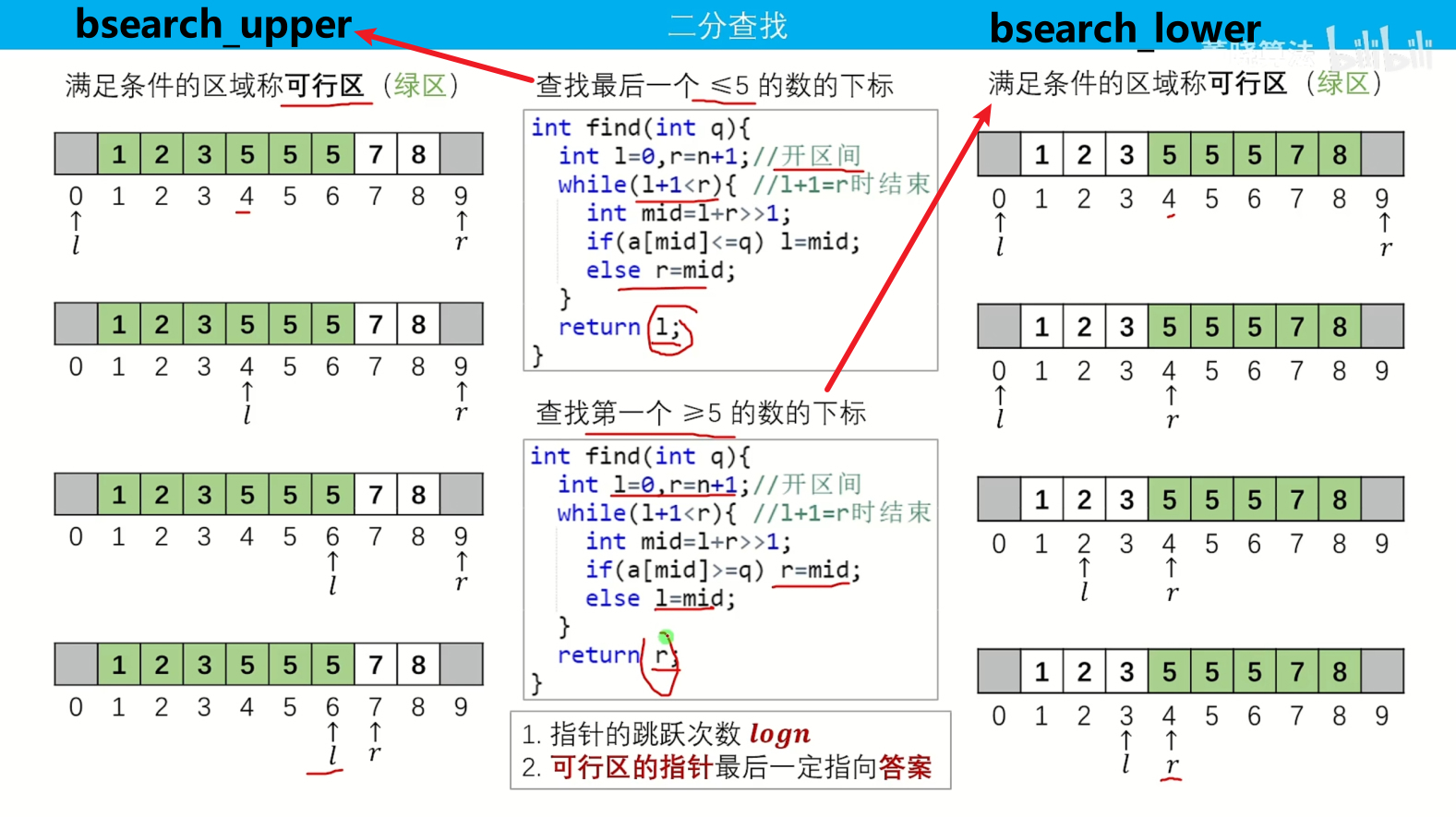
$fileName

2. 注意点：

Q： 为什么必须是开区间？
A： 反证法：
如图，如果要查找最后一个 <= 8 的数的下标，让 l 和 r 初值指向闭区间，为 1 和 8，在模拟过程中，我们会发现最后条件结束时，l = 7，退出循环，但是此时还没有找完。

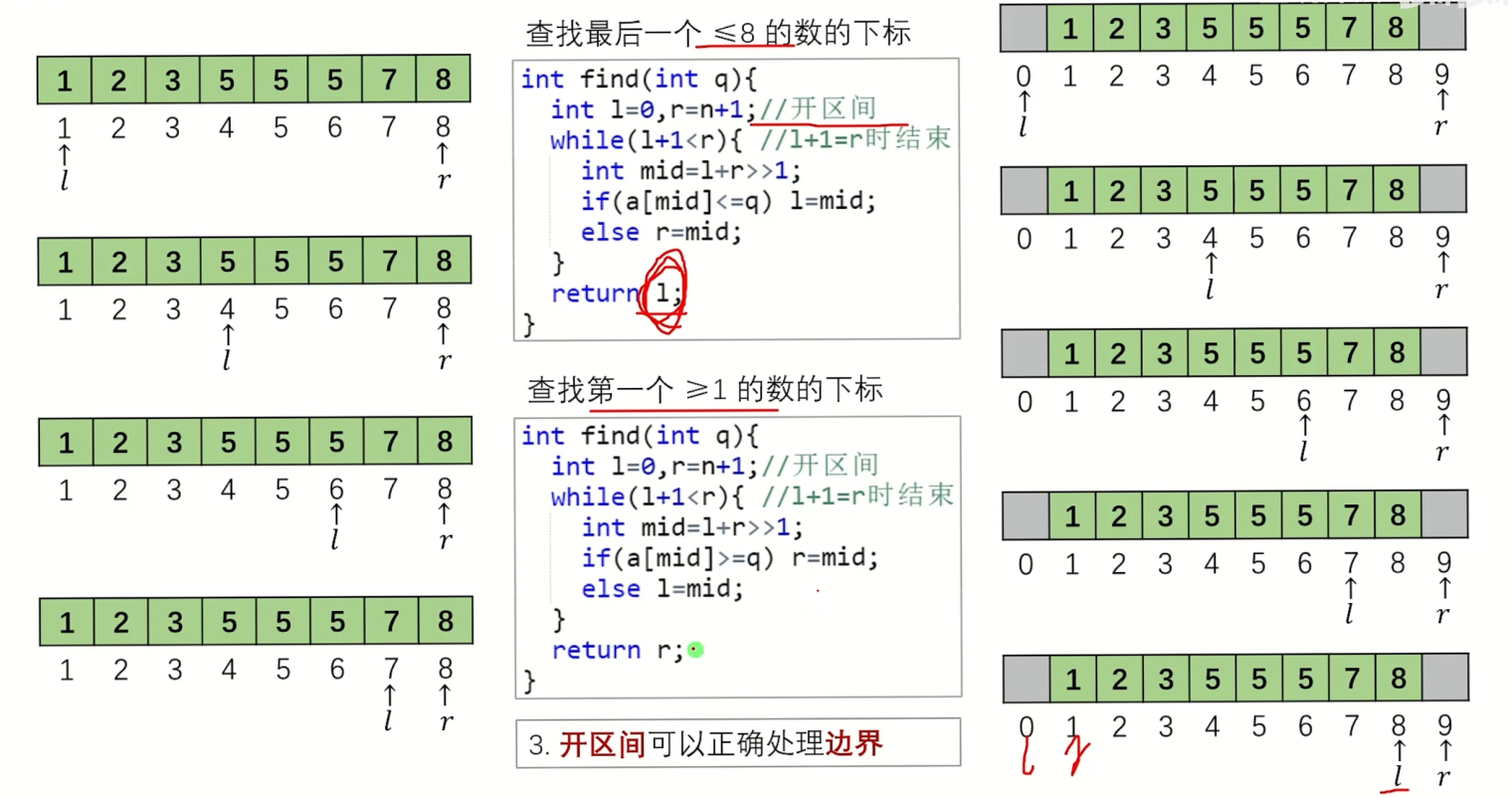
$fileName

3. 总结：

很容易发现，这两种写法是对称的，而且从图中也能很好的看出来：

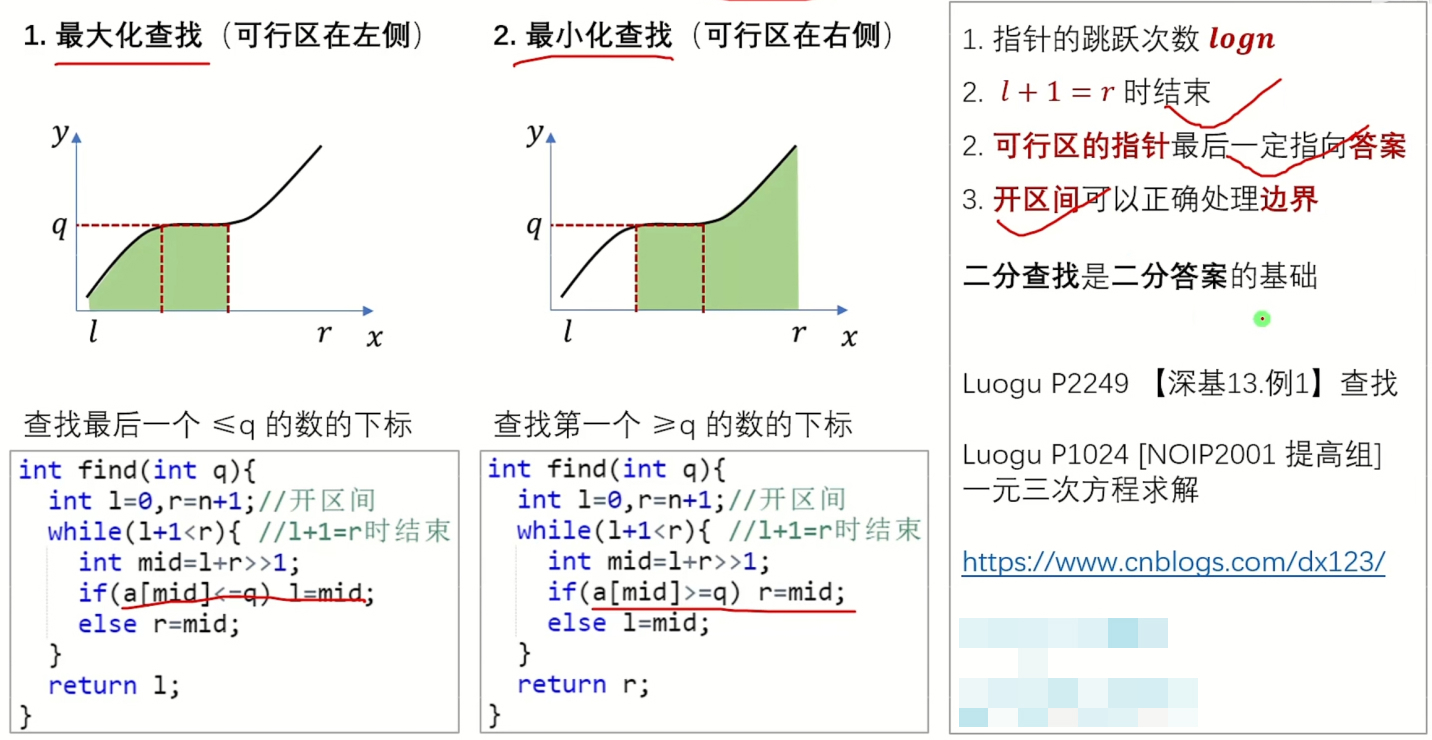
$fileName

4. 代码模板：

注意：以查询上限和下限为例。
这两个函数的 check() 函数不一定相同，根据题目设计。

  1. 左开右开 (-1, n)
  2. 数组下标从 -1 开始，到 n 结束
  3. 默认升序排列
    如果是降序，把 >= 改为 <=**，把 **<=** 改为 **>=
bool check(int mid, int x) {/* ... */}   // 检查 x 是否满足某种性质

// 最小化查找 ( 可行区在右侧 ) : 查找第一个满足 check(mid, x) 的数的下标
int bsearch_lower(int l, int r, int x){
    while (l + 1 < r){          // l + 1 = r时结束
        int mid = l + (r - l) / 2;
        if (check(mid, x)) r = mid;
        else l = mid;
    }
    return r;
}

// 最大化查找 ( 可行区在左侧 ) :查找最后一个满足 check(mid, x) 的数的下标
int bsearch_upper(int l, int r, int x){
    while (l + 1 < r){          // l + 1 = r 时结束
        int mid = l + (r - l) / 2;
        if (check(mid, x)) l = mid;
        else r = mid;
    }
    return l;
}

五、浮点数二分

  1. double 可以直接除而不会取整，所以不用在意边界问题，较为简单。即不需要考虑 mid 是否 +1 ，else 后是否 +1。
  2. 判断条件一般为 r - l >= 1e-6.
    没有固定的浮点数序列，因此要考虑精度 eps，一般比题目要求多 2 位小数就行
  3. 需要自己确定l和r的值，即查找范围
  4. 或者不使用函数，改为 for 循环，相当于除了 2^100 次方，效果跟 r - l > eps 是一样的。
bool check(double mid, double x) {/* ... */} // 检查x是否满足某种性质

double bsearch(double l, double r){
    const double eps = 1e-6;   // eps 表示精度, 一般比题目要求多 2 位即可
    while (r - l > eps){
        double mid = (l + r) / 2;
        if (check(mid, x)) r = mid;
        else l = mid;
    }
    return l;
}