第一讲 基础算法 - 02 归并排序

[toc]

归并排序

一、简介

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：

  1. 自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）；
  2. 自下而上的迭代；

二、算法步骤

菜鸟教程：

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
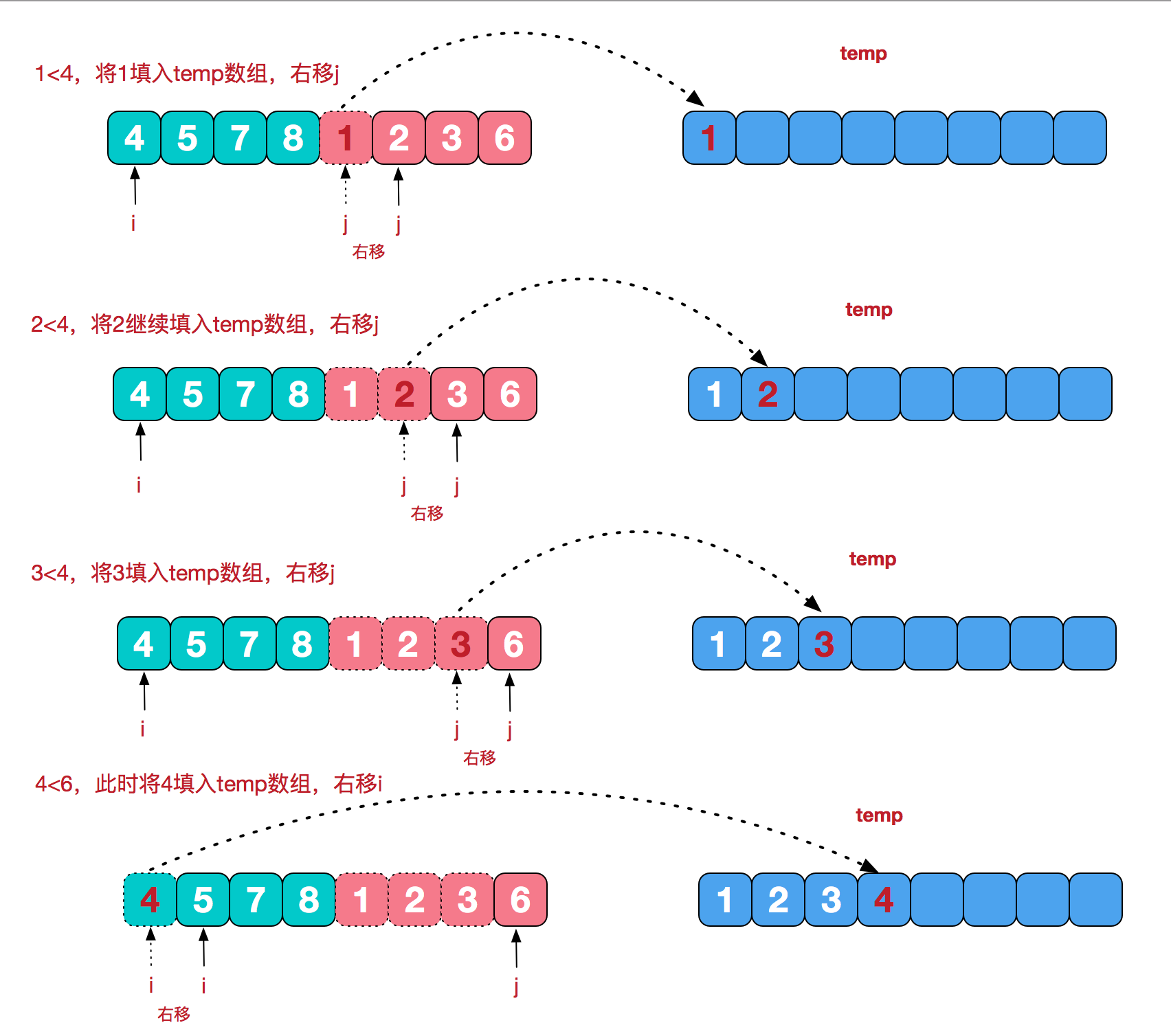
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  4. 重复步骤 3 直到某一指针达到序列尾；
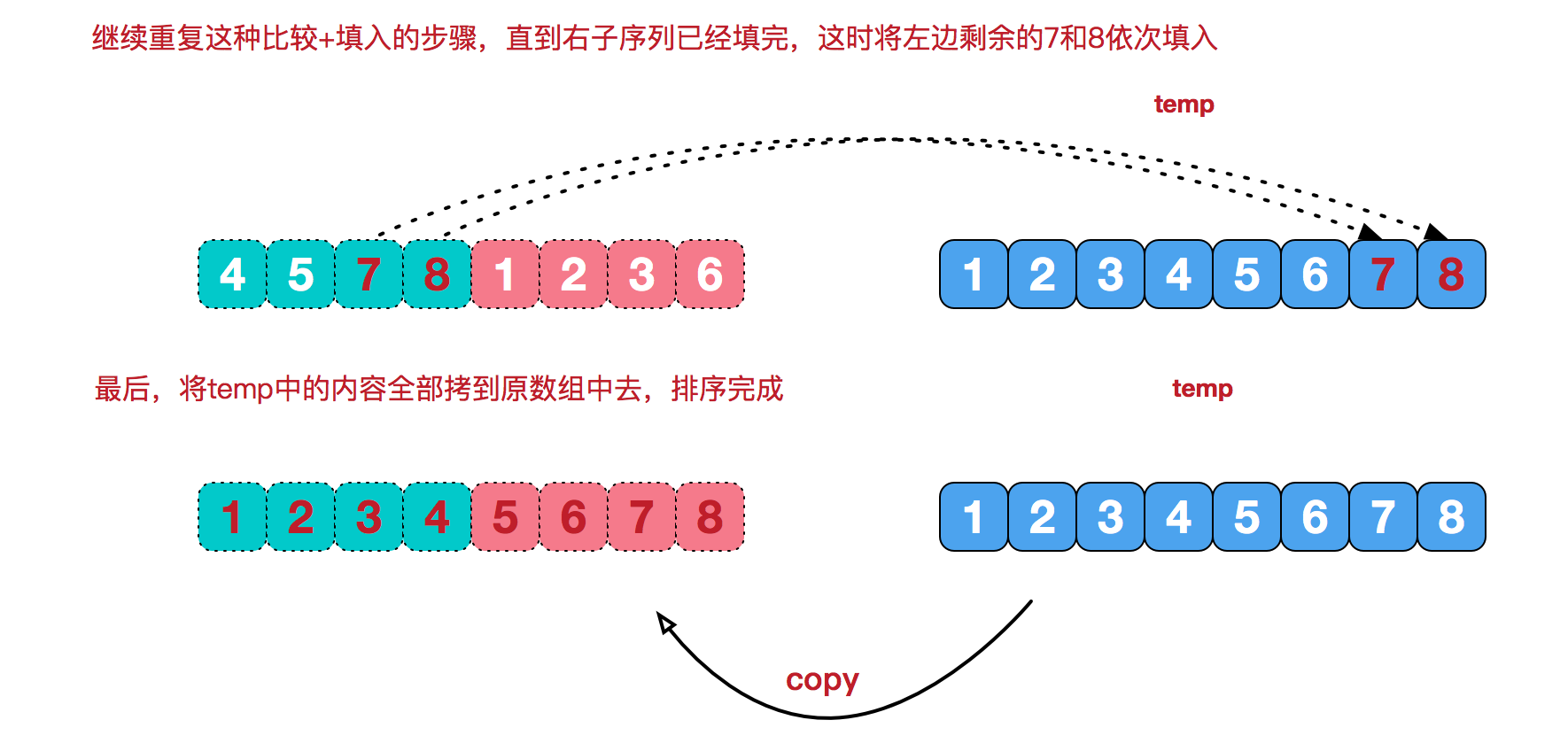
  5. 将另一序列剩下的所有元素直接复制到合并序列尾。

gif

三、基本思想

基于分治，以中间为分界。

  1. 确定分界点 mid = (l + r) / 2
  2. 递归处理左右两段
  3. 归并——合二为一（双指针算法，指针表示剩余部分中最小元素的位置）（较难部分）

1

四、实例说明

Q： 归并排序的第二步递归排序左右两段是怎么实现的？为啥递归后就有序了？是什么原理？
A： 纸上画一下你就理解了，递归相当于一个树形的结构，归并排序的话先递归，递归到最后一层就是树的叶子结点，也就是数组中的单个元素，不需要比较，然后返回上层，就是两个元素，然后排序这两个元素，然后再返回上层递归，依次类推，这样就能排好序了。

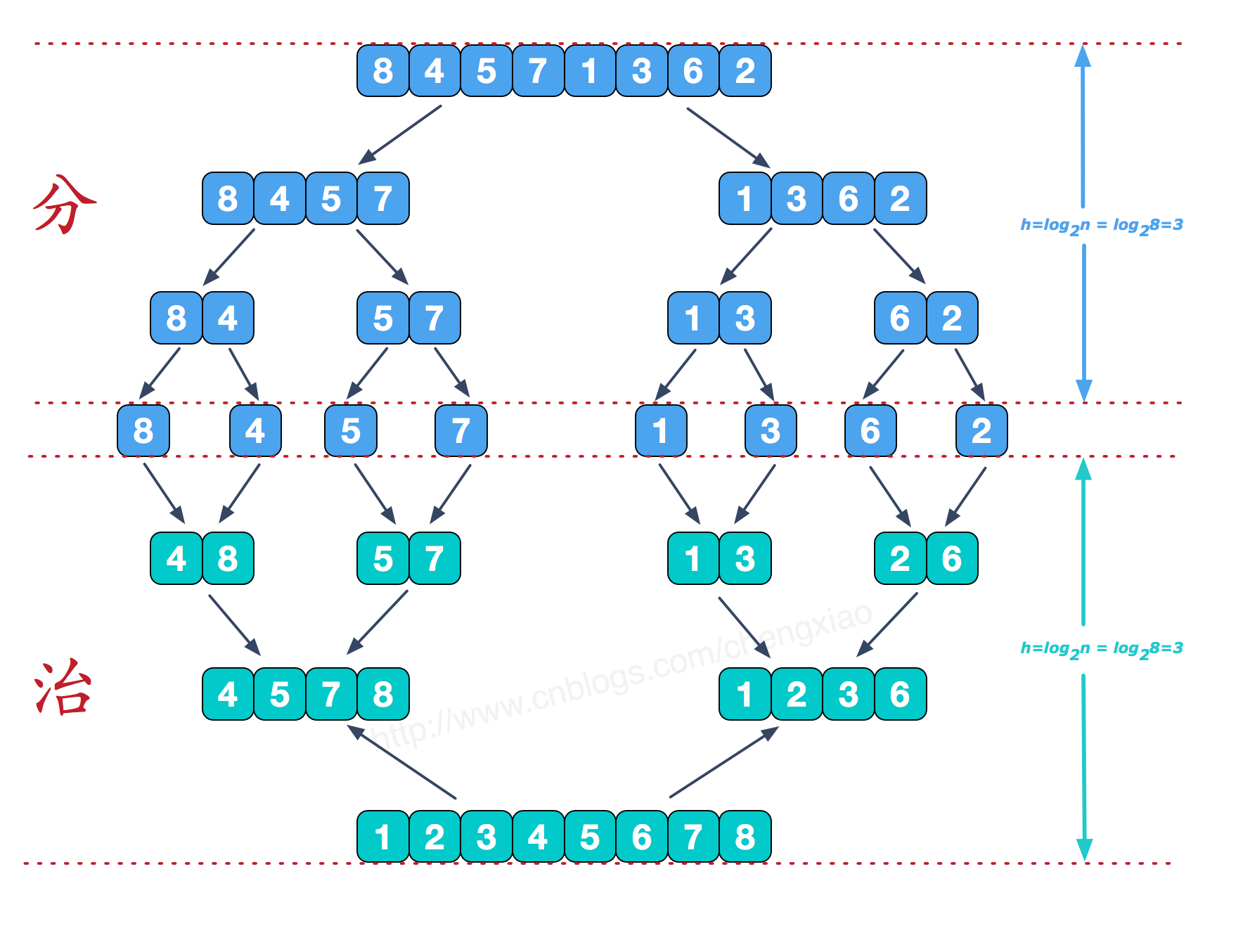
如下图所示：

2

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分 阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

合并相邻有序子序列
再来看看 治 阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将 [4,5,7,8] 和 [1,2,3,6] 两个已经有序的子序列，合并为最终序列 [1,2,3,4,5,6,7,8]，来看下实现步骤。

3
4

五、代码模板

注意：
在归并步骤时，如果碰到相同元素的插入，每次都选择第1段（左边）的元素插入，则能使归并算法稳定。

int tmp[N];

void merge_soft(int q[], int l, int r){
    if (l >= r) return;   // 基本情况：如果左边界大于等于右边界，则返回
    
    int mid = (l + (r - l) / 2);
    merge_soft(q, l, mid);
    merge_soft(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;  // 初始化用于合并的变量
    while (i <= mid && j <= r)      // 比较左右两半的元素，按顺序合并到临时数组 tmp 中
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];
    
    while (i <= mid) tmp[k ++ ] = q[i ++ ];  // 处理左半段中剩余的元素（如果有）
    while (j <= r) tmp[k ++ ] = q[j ++ ];    // 处理右半段中剩余的元素（如果有）
    
    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];  // 将合并后的元素复制回原数组
}

Q： 最后一步合并后的元素复制回原数组是怎么实现的？初始化条件是怎么设置的？
A： 这段代码是在归并排序的最后阶段，将排好序的临时数组 tmp 中的元素复制回原始数组 q 中。在归并排序的过程中，数组被分割和合并，最终需要将合并后的结果放回原数组，以完成整个排序过程。
具体来说，这个循环的作用是将 tmp 数组中的元素按顺序复制回原数组 q。循环的初始条件是 i 等于左边界 l，而 j 则从 0 开始。在每一次迭代中，将 tmp[j] 复制到 q[i] ，然后分别增加 i 和 j 的值。这个过程一直持续，直到 i 大于右边界 r。
这样，经过这个循环，排好序的元素就被正确地放回到原数组 q 中，完成了整个归并排序的过程。