数据结构 - 链表作业2: 约瑟夫环 (三种方法) (猴子选大王)

Akari2024-03-062024-03-09

懒猫老师-C语言-链表作业2:约瑟夫环(三种方法)(猴子选大王)_哔哩哔哩_bilibili

1 什么是约瑟夫环

OpenJudge - 1748:约瑟夫问题

题目描述
约瑟夫问题：有ｎ只猴子，按顺时针方向围成一圈选大王（编号从１到ｎ），从第１号开始报数，一直数到ｍ，数到ｍ的猴子退出圈外，剩下的猴子再接着从1开始报数。就这样，直到圈内只剩下一只猴子时，这个猴子就是猴王，编程求输入ｎ，ｍ后，输出最后猴王的编号。

输入
每行是用空格分开的两个整数，第一个是 n, 第二个是 m ( 0 < m,n <=300)。最后一行是：
0 0

输出
对于每行输入数据 (最后一行除外) ，输出数据也是一行，即最后猴王的编号

样例输入:

6 2
12 4
8 3
0 0

样例输出:

5
1
7

2 约瑟夫环的四种实现方法

2.1 循环链表实现

2.1.1 图解

1. 采用循环链表的原因

如图, 构建一个链表, 这个链表的尾部指向开头, 形成一个循环链表, 依次形成一个猴子的约瑟夫环是非常合适的.

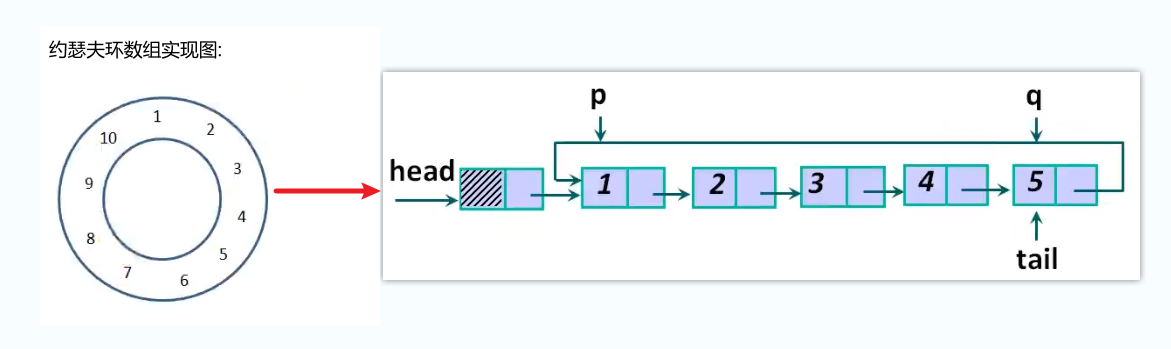
2. 尾插法构建循环链表

for (i = 0; i < n; i ++ ) {
    p = (struct node *)malloc(sizeof(struct node));
    p->data = i + 1;        // 保存猴子的编号
    tail->next = p;         // 插到尾部
    p->next = head->next;   // 尾节点的 next 域指向第一个有效节点, 形成循环链表
    tail = p;       // 更新尾节点
}

如图, 一开始 head 和 tail 都指向头结点, 当 i = 0 时, 插入 p->data = 1 , 最终结果如图所示:

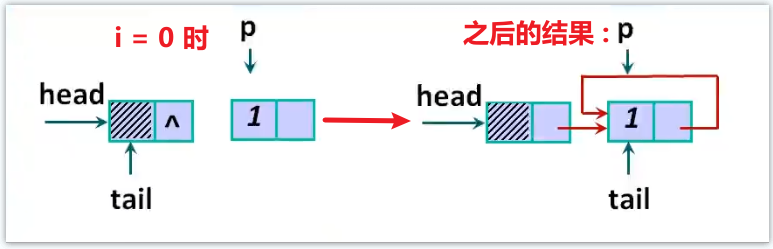
遍历之后构建一个完整的循环链表, 并初始化 p, q 指针到正确的位置 : p 指向当前处理的节点, q 指向 p 的前一个节点, 即 tail. 并且 p, q 总是保持一前一后的关系, 为之后的查找做准备.

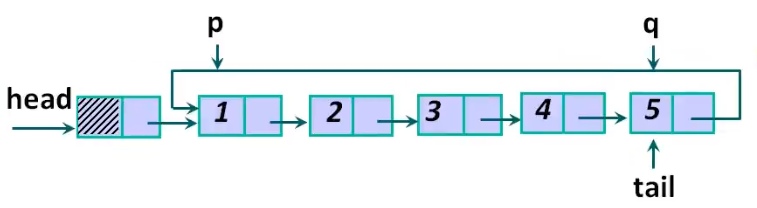
3. 模拟报数

while (p != q) {        // p, q 总是一前一后, 一旦相遇, 说明只剩一个节点
    if (i == m) {
        q->next = q->next->next;    // 删除当前节点, 等价于 p = p->next;
        free(p);
        p = q->next;    // p 移动到下一个有效节点
        i = 1;          // 已找到, 重新开始报数
    }
    else {
        q = p;          // p, q 各自后移一个节点, 并且 q 在 p 的前面
        p = p->next;
        i ++ ;          // 未找到, 报数 + 1
    }
}

当 p = q 时, 循环结束.
当 i = m 时, 即报数达到 m ，删除 p 指向的节点，将 q 的下一个节点指向 p 的下一个节点。
当 i != m 时, 即报数未达到 m , 将 p 移动到下一个未被删除的节点，q 也相应移动，继续重复报数和删除的过程。

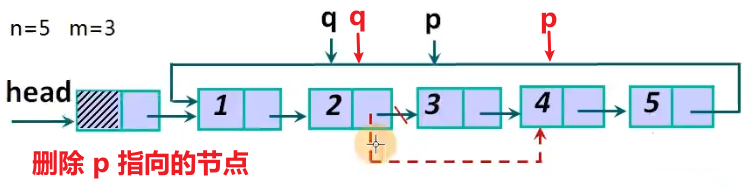
4. 收尾处理

head->next = q;
ans[count ++ ] = p->data;   // ans 数组保存数组下标
free(p);
head->next = NULL;          // 清空链表, 保留头结点, 且 next = NULL

注意:

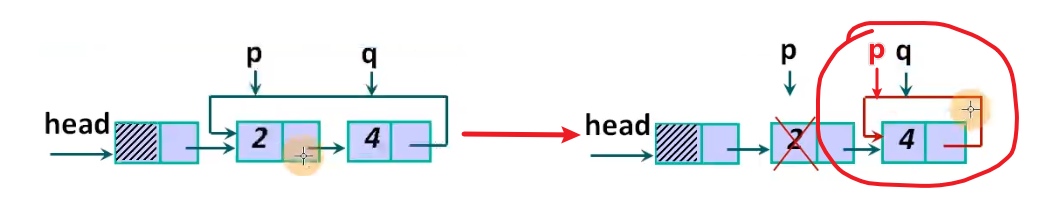
前面删除节点时, 当最后只剩最后一个节点, 删除第一个节点时, 会造成链表不完整, 所以要加上 head->next = q; , 或者 head->next = p;
需要特别注意最后一个节点被删除后, 要将头节点的 next 指针置为 NULL , 否则可能会导致内存访问越界等问题。如图:

2.1.2 思路

这个程序的主要思路是使用循环链表来模拟 “约瑟夫环” 问题。

思路

首先使用尾插法创建一个包含 n 个节点的循环链表，每个节点存储一个编号表示一只猴子。
设置两个指针 p 和 q，分别指向当前需要删除的节点和它的前一个节点。
开始从 p 指向的节点开始报数，当报数达到 m 时，删除 p 指向的节点，将 q 的下一个节点指向 p 的下一个节点。
将 p 移动到下一个未被删除的节点，q 也相应移动，继续重复报数和删除的过程。
当 p 和 q 相遇时，说明只剩下最后一个节点，记录下这个节点的编号。
重复上述过程，直到输入为 0 0 时结束。
最后输出所有被删除节点的编号。

关键点

使用循环链表来模拟环形结构。
利用两个指针 p 和 q 来跟踪当前节点和前一个节点,方便进行节点删除操作。
通过循环不断报数和删除节点, 直到只剩一个节点为止。
记录每次删除节点的编号, 最后输出。
这种方法的时间复杂度为 *O(nm)**，空间复杂度为 **O(n)**。

注意点

内存管理
- 程序中使用了动态内存分配 (malloc) 来创建链表节点, 因此需要在适当的时候 (比如循环结束或者输入为 0 0 时) 使用 free 释放已分配的内存,避免内存泄漏。
- 需要特别注意最后一个节点被删除后, 要将头节点的 next 指针置为 NULL , 否则可能会导致内存访问越界等问题。
边界条件处理
- 当输入为 0 0 时, 需要正确地释放已分配的内存并退出程序。
- 当只剩最后一个节点时, 需要正确地处理, 避免出现野指针等问题。
链表操作
- 创建循环链表时, 需要正确地设置最后一个节点的 next 指向头节点。
- 删除节点时, 需要正确地修改前一个节点的 next 指针, 并释放被删除节点的内存。
- 移动指针 p 和 q 时,需要注意它们之间的相对位置关系。
程序逻辑
- 正确实现报数和删除节点的逻辑, 确保每报到 m 就删除当前节点。
- 正确记录被删除节点的编号, 以便最后输出。

总的来说, 这个程序涉及到动态内存管理、链表操作、程序逻辑控制等多个方面, 需要格外注意各种边界情况和异常处理, 以避免内存泄漏、野指针等问题。

2.1.3 代码

#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>

struct node{
    int data;
    struct node *next;
};

int main(void)
{
    int n, m;
    int i;          // 报数
    int ans[100];   // 保存答案的桶
    int count = 0;  // 控制答案的下标
    struct node *head, *tail, *p, *q;   // p 指向当前处理的节点, q 指向 p 的前一个节点
    
    head = (struct node *)malloc(sizeof(struct node));
    head->data = -1;
    head->next = NULL;
    
    while (~scanf("%d %d", &n, &m)) {
        if (n == 0 || m == 0) {
            free(head);     // 输入结束, 必须释放 malloc 结点的内存
            break;
        }
        else {
            tail = head;
            
            /* 尾插法构建循环链表 */
            for (i = 0; i < n; i ++ ) {
                p = (struct node *)malloc(sizeof(struct node));
                p->data = i + 1;        // 保存猴子的编号
                tail->next = p;         // 插到尾部
                p->next = head->next;   // 尾节点的 next 域指向第一个有效节点, 形成循环链表
                tail = p;   // 更新尾节点
            }
            
            /* 初始化临时变量, 为模拟报数做准备 */
            p = head->next;
            q = tail;               // q 是 p 的前驱节点, 即 tail
            i = 1;
            
            /* 循环, 选大王 */
            while (p != q) {        // p, q 总是一前一后, 一旦相遇, 说明只剩一个节点
                if (i == m) {
                    q->next = q->next->next;    // 删除当前节点, 等价于 p = p->next;
                    free(p);
                    p = q->next;    // p 移动到下一个有效节点
                    i = 1;          // 已找到, 重新开始报数
                }
                else {
                    q = p;          // p, q 各自后移一个节点, 并且 q 在 p 的前面
                    p = p->next;
                    i ++ ;          // 未找到, 报数 + 1
                }
            }
            
            head->next = q;             // 前面删除节点时, 当最后只剩最后一个节点, 删除第一个节点时, 会造成链表不完整, 但本题无要求
            ans[count ++ ] = p->data;   // ans 数组保存数组下标
            free(p);
            head->next = NULL;          // 清空链表, 保留头结点, 并且 next = NULL
        }
    }
    
    for (i = 0; i < count; i ++ )
        printf("%d\n", ans[i]);
    free(head);
    
    return 0;
}

2.2 数组标志位实现

2.2.1 图解

1. 模拟图

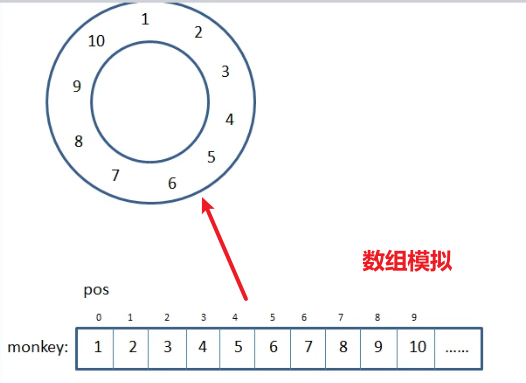
2. 模拟报数猴子

最后只剩下一个猴子的状态:

2.2.2 思路

这个程序使用数组模拟”约瑟夫环”问题的解决过程。

思路

使用一个长度为 310 的整型数组 monkey[310] 来存储猴子的编号和状态。初始时将猴子的编号 1~n 存入数组的前 n 个位置。
使用一个变量 pos 来控制当前处理的数组下标, 初始化为 0。
使用一个变量 count 来记录当前报数, 初始化为 1。
使用一个变量 number 来记录剩余猴子的数量, 初始化为 n。
进入一个循环, 每次让 pos 指向的猴子报数, 如果报数等于 m , 就让该猴子出局 (将它在数组中的值设为 0) , 并重置 count 为 1 , 剩余猴子数量 number 减 1。
如果报数不等于 m , 就将 count 加 1, 并让 pos 移动到下一个未出局猴子的位置。
循环执行直到只剩一个猴子为止 (number = 1 )。
最后遍历数组, 输出所有值不为 0 的位置, 即为最后剩下的猴子编号。

关键点

使用数组来模拟猴子的排列顺序和状态。
使用变量 pos 控制当前报数的猴子位置, count 记录报数。
根据报数是否等于 m 来决定是否让当前猴子出局。
通过循环不断更新猴子状态, 直到只剩一个为止。
最后遍历数组输出剩余的猴子编号。

这种方法的时间复杂度为 O(n*m), 空间复杂度为 **O(n)**。

注意点

数组下标越界
- 在更新 pos 的值时,使用了取模运算 (pos + 1) % n ,这样可以确保 pos 的值在 [0, n-1] 范围内循环。但需要注意当 n 等于 0 时, 取模运算会出现除以 0 的错误, 因此在主循环开始前需要判断 n 是否为 0 。
数组元素初始化
- 程序中使用了一个长度为 310 的数组 monkey[310] , 其中只使用了前 n 个元素。为避免出现未初始化的数组元素, 可以在初始化时将整个数组元素都设置为 -1 , 表示无效内容。
内存使用
- 这个程序仅使用了一个长度为 310 的数组, 没有动态分配内存, 因此不需要特别注意内存管理的问题。但如果数组长度不够, 就需要使用动态分配的方式, 这时需要注意内存释放的问题。

总的来说, 这个程序相对于链表实现方式, 代码结构更加简洁, 但也需要注意一些细节问题, 如数组下标、输入合法性等, 以免出现逻辑错误或者非预期的运行结果。

2.2.3 代码

#include <stdio.h>

int main(void)
{
    int n, m;
    int number;         // 保存剩余的猴子个数
    int count = 1;      // 记录当前报数
    int pos = 0;        // 控制当前处理的数组下标
    int monkey[310] = {-1};      // monkey[310] 数组保存猴子的编号和状态
                                // -1 代表无效内容, 0 代表退出的猴子, 1 ~ n + 1 代表未退出
    
    while (~scanf("%d %d", &n, &m)) {
        if (n == 0 || m == 0)
            return 0;

        number = n;
        for (int i = 0; i < n; i ++ )
            monkey[i] = i + 1;
        
        pos = 0;    // 初始化下标为 0
        while (number > 1) {
            if (monkey[pos] > 0) {
                if (count != m) {
                    count ++ ;              // 未找到报数 + 1
                    pos = (pos + 1) % n;    // 当前处理的数组下标 + 1
                }
                else {
                    monkey[pos] = 0;        // 已找到, 标记为 0, 使其出局
                    count = 1;              // 重新开始报数
                    number -- ;             // 猴子数量 - 1
                    pos = (pos + 1) % n;    // 当前处理的数组下标 + 1
                }
            }
            else    // monkey[pos] = 0
                pos = (pos + 1) % n;        // 当前处理的数组下标 + 1
        }
        
        // 接着遍历数组, 找到 monkey[i] 不为 0 的猴子并输出
        for (int i = 0; i < n; i ++ )
            if (monkey[i] > 0)
                printf("%d\n", monkey[i]);
    }
    
    return 0;
}

2.3 数组链接方式实现

2.3.1 图解

图解

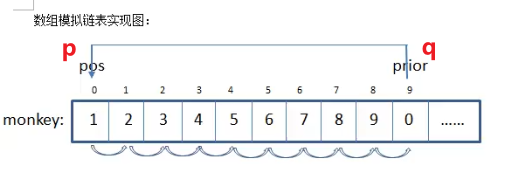
数组模拟循环链表实现图

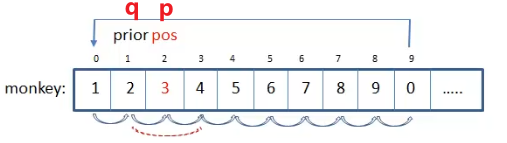
2.3.2 思路

这个程序使用数组模拟链表的方式来解决约瑟夫环问题。可以将约瑟夫环问题看作是一个环形链表, 每次需要删除第 m 个节点。

思路

使用一个长度为 310 的整型数组 monkey[310] 来模拟链表。数组的每个元素存储下一个节点的下标, 形成一个循环链表。
初始化数组时, 将前 n - 1 个元素的值设为下一个节点的下标, 最后一个元素的值设为 0, 指向数组开头, 构成循环链表。
使用三个变量 p、q 和 count 分别跟踪当前节点、当前节点的前一个节点和当前报数。
进入循环
- 若 count != m , 则 p 移动到下一个节点, q 也相应移动, count ++ 。
- 若 count == m , 则将 q 指向 p 的下一个节点, 把 p 对应的数组元素值设为 -1 (表示出局), p 移动到下一个未出局节点, count 重置为 1 , 剩余节点数 number -- 。
- 循环执行直到只剩一个节点为止 (number == 1)。
输出最后剩下节点的编号 (p + 1) 。

这种思路只需要一个一维数组和几个整型变量即可实现, 复杂度为 *O(nm)**。相比之前的做法, 思路更加简单直接, 代码实现也会更加简洁。但需要注意数组下标越界的问题。

注意点

在实现这个程序时, 需要注意以下几个方面:

数组初始化
- 程序对数组 monkey[310] 的初始化是将前 n - 1 个元素设置为下一个节点的下标, 最后一个元素设置为 0, 指向数组开头。
- 需要注意的是, 数组剩余的元素都是 0, 在链表模拟的过程中, 需要区分 0 是有效值还是未初始化的值。一种解决方案是在初始化时将剩余元素设置为 -1 或其他特殊值。
边界条件处理
- 当输入 n 或 m 为 0 时, 程序直接返回, 没有进行其他操作。这可能会导致一些潜在的问题, 比如内存泄漏 (如果使用了动态内存分配) 。
- 另外, 当 n = 1 时, 程序输出 1, 但实际上应该直接退出, 因为只有一个猴子时, 不需要进行环操作。

总的来说, 这个程序相对于链表实现方式, 代码更加简洁, 但也需要注意一些细节问题, 如数组长度、边界条件处理、输出格式等, 以确保程序的正确性和 robust 性。同时, 良好的代码风格和注释也是很重要的。

2.3.3 代码

#include <stdio.h>

int main(void)
{
    int n, m;
    int number;     // 记录剩余的猴子个数
    int count;      // 代表当前的报数
    int i, p, q;    // p: pos   q: prior
    
    while (~scanf("%d %d", &n, &m)){
        if (n == 0 || m == 0)
            return 0;
        
        int monkey[310] = {0};      // 初始化数组, 数组存储下一个猴子的下标, -1 代表已退出
        for (i = 0; i < n - 1; i ++ )
            monkey[i] = i + 1;
        monkey[i] = 0;              // 下标为 n - 1 的元素的下个序号为 0 , 形成循环链表
        // monkey[i + 1] = -2;      // 将超过范围的元素标识为 -2, 方便跟踪的时候看数组内存

        number = n;
        p = 0;
        q = n - 1;
        count = 1;
        while (number > 1) {        // 或者不需要 number 计数, 将退出条件设为 prior != pos
            if (count != m) {
                q = p;              // prior 保存 pos 的上一个节点的下标
                p = monkey[p];      // pos 移动到下一个有效节点的下标
                count ++ ;
            }
            else {
                monkey[q] = monkey[p];  // 更改链接关系
                monkey[p] = -1;         // 出局, 标识设为 -1
                p = monkey[q];          // pos 移动到下一个有效节点的下标
                number -- ;
                count = 1;
            }
        }
        printf("%d\n", p + 1);
    }
    
    return 0;
}